Accurate clinical decision making requires, among many other factors, an ability to estimate probability of disease or prognosis given a particular history and findings of a physical examination. This estimate, termed the “pre-test probability”, is modified by the results of diagnostic tests to arrive at a “post-test probability” of disease. There is often sufficient information to help clinicians interpret diagnostic tests — their characteristics are described in terms of sensitivity or specificity, positive or negative predictive values, or, more recently, likelihood ratios.1,2 By contrast, there is often little objective guidance for clinicians estimating pre-test probabilities.3 Although a few clinical-decision rules exist, they are rare, and most discussions of this problem end with some reassurance that clinical experience will resolve this problem. A prominent textbook in the area states:4
This assertion has not been rigorously tested, and, if it is not correct, the consequences for patient outcomes would be serious. Falsely low pre-test probabilities may lead to extra diagnostic tests or lack of treatment, whereas falsely high pre-test probabilities may lead to unnecessary treatment.
Questions of prognosis raise similar issues. The decision about whether to treat depends not only on the relative risk reduction found in clinical trials, but on the baseline risk of the outcome in a particular patient (allowing absolute risk reduction to be calculated), which may be as difficult to estimate as the pre-test probability.
Many studies have investigated clinicians’ estimates of diagnostic probabilities. For example:
comparing predicted probability in actual patients to a reference standard (eg, the probability of coronary artery disease compared with diagnostic findings of coronary angiography);5
comparing predicted probability in actual patients during examination with a written scenario of the same information;6
exploring healthcare professionals’ intuitive ability to increase or decrease the pre-test probability given a positive or negative test result, compared with a formal calculation using Bayes’ nomogram;7
comparing predicted pre-test probabilities in actual patients to a reference standard.8
By and large these studies all indicate a poor degree of accuracy and wide variability. In many cases, however, these studies are small, use a convenience sample, and relate accuracy to patient, rather than clinician, variables.
We assessed the accuracy and variability of clinicians’ estimates of pre-test probabilities, compared with estimates derived from clinical-decision rules, in a large random sample of general practitioners and physicians (both generalists and specialists), and related the results to clinicians’ characteristics.
We chose three clinical scenarios which were common enough to be familiar to GPs and physicians, and for which there were validated clinical-decision rules for generating pre-test probabilities: the first two were diagnostic questions — risk of ischaemic heart disease (IHD),9 and risk of deep vein thrombosis (DVT),10 respectively — and the third was a prognosis question regarding baseline risk of future stroke in atrial fibrillation11 (Box 1). Participants were asked to judge pre-test probabilities as a continuous variable (0–100%). We also collected demographic and educational factors, including age, sex, practice profile, specialty, and postgraduate study.
Australia: The questionnaire was mailed to 500 physicians (randomly chosen from the membership list of the Royal Australasian College of Physicians) and 500 general practitioners (randomly chosen from the roster of the Royal Australian College of General Practitioners) all residing in New South Wales. A reminder was sent to non-respondents after 2 months. There was no financial incentive for participating, but the physicians were able to claim continuing medical education points from their College. All clinicians were provided with feedback on the scenarios, with a short synopsis, the clinical-decision rule, and the reference to the article in which the clinical-decision rule appeared (see, as an example, feedback on Scenario 1 [Appendix, page 453]).
UK: Questionnaires with the same scenarios were sent to 205 physicians (randomly selected from members and fellows of the Royal College of Physicians in north-west England) and 202 GPs (randomly chosen from the practice lists held by the Manchester Health Authority). One reminder was sent to non-respondents 2 weeks later, and respondents received the same feedback as in Australia.
In both countries the study was conducted between April and October 2001.
We analysed accuracy by determining the frequency of clinicians’ estimates within 10, 20, or 30 percentage points of, and more than 30 percentage points away from, the “correct” estimate (ie, the one predicted by the clinical-decision rule). Descriptive statistics (“box-and-whisker plots”) were used to describe the variability of estimates. To explore which factors were related to variability, statistical modelling was performed using linear regression, with the outcome variable being the difference between the “correct” response and clinicians’ estimates. Where appropriate, χ2 tests were adjusted for multiple comparisons. Analyses, both univariate and multivariate, were performed using the statistical package JMP.12
There were 598 respondents (60%) to the Australian questionnaire, and 221 respondents (57%) to the UK questionnaire. The demographic, specialty and educational characteristics of the respondents are given in Box 2.
Box 3 shows the proportion of responses within 10, 20, and 30 percentage points of the correct response for each scenario. Overall, Australian respondents performed well on Scenario 1 (chest pain and risk of IHD) and Scenario 3 (atrial fibrillation and risk of stroke), with 54% and 57% of responses being within 20 percentage points of the correct estimate. However, they did not do well on Scenario 2 (DVT), with only 6.7% being within 20 percentage points of the correct estimate.
UK respondents’ results were similar to the Australian results for Scenarios 1 and 2, with 48% and 12%, respectively, being within 20 percentage points of the correct estimate. However, UK respondents scored significantly better than Australian respondents for Scenario 3, with 65% being within 20 percentage points of the correct estimate (χ2 = 24.2; P < 0.001).
In the Australian arm of the study, cardiologists’ results were similar to those of physicians in other subspecialties (“other physicians”), who, in turn, were significantly more accurate than GPs across all three scenarios (χ2 test, P < 0.001, P = 0.012, and P < 0.001 for Scenarios 1, 2 and 3, respectively [Box 4]).
There was a large spread of pre-test probability estimates given for each scenario. The spread of estimates, as measured by the interquartile ranges, was similar between scenarios and between the Australian and UK groups (Box 5). Respondents’ estimates for all scenarios ranged from about 5% to 100%. The spread of estimates was as wide among cardiologists as among the other two groups — GPs and “other” physicians.
Multiple linear regression was used to provide predictive models for each of the three scenarios (Box 6). Only two factors were consistently found to approach or reach statistical significance across all three scenarios — postgraduate training was associated with less accuracy, and being a physician other than a cardiologist with more accuracy. We failed to find any statistically significant predictors in the analysis of the UK group, probably due to the smaller sample size and to the fact that information on fewer variables was collected.
However, the regression models for each scenario were very poor, with R2 values ranging from 5% to 7% (Box 6). This implies that there are other factors, not assessed by the questionnaire, that would better predict the likelihood of a correct response.
There was no consistent pattern of over- or underestimation by individual respondents. They may have overestimated on one scenario, and underestimated on another.
The accuracy of pre-test probability estimates for these common clinical scenarios was fair to poor. About 55% of doctors provided pre-test probability estimates within 20 percentage points of the “correct” estimate for two common clinical scenarios (chest pain and risk of IHD; and atrial fibrillation and risk of stroke), but a substantially lower percentage (7% and 12%, respectively, for the Australian and UK respondents) were within this range for the DVT scenario. The poorer performance on the latter scenario is probably due to the mention of some asymmetrical leg swelling that did not meet the minimum threshold specified by the clinical-decision rule (2 cm v 3 cm), but which may have led to an overestimation of the pre-test probability.
We are aware of the limited number and breadth of these scenarios. The reasons for choosing these scenarios — they were common enough to be familiar to both GPs and physicians, and well-validated clinical-decision rules were available — have already been mentioned; and we limited the number to three to reduce the burden of completing the questionnaire and to maximise participation.
The strengths of our study are the standardised methods, the large sample size, and the random ascertainment of a representative group of clinicians (drawn from Royal College or area health service lists rather than a convenience sample).
The results of our study are supported by results of other, similar studies. For example, one study comparing physicians’ assessment of heart disease risk after exercise stress tests versus various clinical-decision rules found the clinical-decision rules consistently outperformed even expert clinicians, although the magnitude of the differences, despite being statistically significant, was smaller than in our study.13 Another study of GPs’ and nurses’ classification of patients’ risk of heart disease found poor accuracy.14 Medical students’ estimates of pre-test probabilities were also found to be inaccurate when compared with estimates using decision rules.15 In addition, although clinicians may know the definitions of sensitivity and specificity, this may not necessarily translate into an ability to apply that knowledge (ie, to interpret diagnostic tests properly given a clinical scenario).16
A worrying observation was that a number of clinicians indicated pre-test probabilities of 100%. This presumably reflects a cautious attitude, assuming that all patients have disease until proven otherwise. This method of operating only works if the tests ordered have powerful negative likelihood ratios, and if these tests indeed give negative results. Overestimation of disease risk leaves clinicians unable to judge false positive test results, and may result in more intervention than necessary and indicate a lack of appreciation for how diagnostic tests influence the probability of disease.
The striking and principal finding of our study is the wide range of probabilities generated by this group of practising clinicians in Australia and the UK. Our study is novel in trying to relate this variability to clinician factors rather than patient or scenario factors. In a multivariate analysis, only two factors were somewhat associated with increasing accuracy: lack of postgraduate training, and being a physician other than a cardiologist. However, the R2 values for all three models were very low, indicating that they explain little of the variance, and are unlikely to be of any clinical significance. Given that one should have at least 10 to 20 data points for each variable in a linear regression, we had sufficient power to detect an effect if one existed.17 We interpret this, as well as the notable lack of any association with experience (as measured by age, years since graduation, or field of specialty — cardiologists did not perform better than other physicians, and had as much variability as other clinicians despite the related nature of these scenarios), as an indication that the factors determining variability have not yet been identified. We speculate that the variability in estimates may be due partly to the lack of “numeracy” skills in previous medical curricula (when older clinicians did their undergraduate training). Although there was a trend towards more accurate responses from doctors with problem-based learning experience (which presumably emphasises “numeracy” more strongly), this was not consistent across scenarios, and our study did not have sufficient power to address this with any degree of confidence. Problem-based learning has been shown to encourage life-long learning.18 However, there are doubts about whether critical-appraisal and evidence-based medicine (EBM) skills (and perhaps “numeracy” skills) taught in undergraduate courses can be sustained into residency and practice years.19 The way in which clinical information is “framed” has also been shown to affect interpretation,20 although in our study all scenarios were presented similarly to all participants.
We believe the greater part of this variability is due to the lack of information regarding pre-test probabilities, and the general paucity of clinical-decision rules for common clinical scenarios. Even with our experience in teaching EBM and performing literature searches, it was time-consuming for us to find the relevant clinical-decision rules for the scenarios we used. If EBM is to influence every clinical decision and clinician, it has to be easily available and accessible.21 In addition, a quick review of current journals indicates that most clinical trials and observational studies express results in relative terms, be they relative risks or odds ratios. Even when absolute rates are given, these are often given as means for the entire study population; thus, there is little information to enable a practising clinician to arrive at an absolute risk estimate for a particular patient.
Our results highlight the lack of attention that has been paid to generating pre-test probabilities. Rather than simply relying on “clinical experience”, research results and data must be expressed in a manner that allows more direct applicability to individual patients, whether in the form of decision rules, or point scores. Although such clinical-decision rules are starting to be published (eg, the Ottawa ankle rules22 and the Canadian C-spine rule23), they are few and far between.
We believe our results can be generalised, as they were consistent in two countries with different healthcare systems and training programs. Our findings indicate a need to develop better methods of generating pre-test probabilities for common clinical conditions, and indeed a need to train clinicians in the appropriate use of pre-test probabilities. This should enhance the accuracy of clinical decision making and lead to more rational use of diagnostic tests and therapies, and better patient care.
1: Three clinical scenarios for assessing the accuracy and variability of general practitioners’ and physicians’ estimates of pre-test probability
Scenario 1
A 65-year-old man presents to the emergency room of your local hospital having had two episodes of retrosternal chest pain today, both precipitated by exertion, but lasting about 2 hours despite rest. Before obtaining the rest of the history or performing a physical examination, what would you estimate his risk of true ischaemic heart disease to be?
“Correct” estimate: 67%
Scenario 2
A 55-year-old woman presents with a painful right calf. She was in hospital for 5 days 3 weeks ago for major surgery (repair of a perforated appendix), and now has a mildly swollen right leg. Her right calf circumference measures 27 cm (v 25 cm on the left), and she has pitting oedema up to her right knee. There is no tenderness over the deep venous system and no dilated superficial veins. What is her risk of having a clinically significant proximal deep-vein thrombosis?
“Correct” estimate: 17%
Scenario 3
A 65-year-old man presents to his family doctor with new-onset atrial fibrillation, which persists over the next month. He is being treated for hypertension with 25 mg hydrochlorothiazide daily (current systolic blood pressure, 140 mmHg), and his electrocardiogram shows voltage criteria for left ventricular hypertrophy. He has no history of diabetes or cardiovascular disease, and is not a smoker. Before prescribing warfarin, what is your estimate of his baseline risk of having a stroke over the next 10 years?
“Correct” estimate: 35%
2: Demographic and educational characteristics of the study respondents
|
Australia (n = 598) |
UK (n = 221) |
|||||||||
GPs |
310 (52%) |
106 (48%) |
|||||||||
Physicians |
288 (48%) |
115 (52%) |
|||||||||
Cardiologists |
42 (15%) |
12 (10%) |
|||||||||
Generalists |
22 (8%) |
14 (12%) |
|||||||||
Other sub-specialties |
224 (78%) |
89 (77%) |
|||||||||
Australian medical school |
494 (83%) |
na |
|||||||||
Overseas medical school |
98 (17%) |
na |
|||||||||
Problem-based learning |
27 (5%) |
na |
|||||||||
Postgraduate degree |
244 (41%) |
105 (48%) |
|||||||||
Years since graduation (mean, SD, range) |
22.6, 10, 3–62 |
22.6, 8.7, 7–51 |
|||||||||
Age (years) (mean, SD, range) |
47.2, 10, 25–83 |
na |
|||||||||
Males |
452 (76%) |
181 (82%) |
|||||||||
Urban practice |
417 (70%) |
na |
|||||||||
Academic practice |
177 (30%) |
na |
|||||||||
na = not available. |
|||||||||||
3: Absolute percentage points difference from the “correct” pre-test probability for the three scenarios, by country
Percentage points difference |
Frequency (%) Australia |
Frequency (%) UK |
|||||||||
Scenario 1 |
|
|
|||||||||
0–9 |
142 (23 8%) |
53 (24.1%) |
|||||||||
10–19 |
178 (29.9%) |
53 (24.1%) |
|||||||||
20–29 |
194 (32.5%) |
73 (33.2%) |
|||||||||
30+ |
82 (13.8%) |
41 (18.6%) |
|||||||||
Total |
596 (100.0%) |
220 (100.0%) |
|||||||||
Scenario 2 |
|
||||||||||
0–9 |
24 (4.0%) |
14 (6.3%) |
|||||||||
10–19 |
16 (2.7%) |
12 (5.5%) |
|||||||||
20–29 |
18 (3.0%) |
6 (2.7%) |
|||||||||
30+ |
539 (90.3%) |
189 (85.5%) |
|||||||||
Total |
597 (100.0%) |
221 (100.0%) |
|||||||||
Scenario 3 |
|||||||||||
0–9 |
149 (25.1%) |
61 (27.9%) |
|||||||||
10–19 |
189 (31.9%) |
82 (37.4%) |
|||||||||
20–29 |
127 (21.5%) |
61 (27.9%) |
|||||||||
30+ |
127 (21.5%) |
15 (6.8%) |
|||||||||
Total |
592 (100.0%) |
219 (100.0%) |
|||||||||
Australian respondents v UK respondents.
Scenario 1: χ23 = 4.5; P = 0.216.
Scenario 2: χ23= 5.9; P = 0.117.
Scenario 3: χ23= 24.2; P < 0.001.
4: The proportion of subjects (95% CIs) in each category of percentage points difference from the “correct” estimate, for each scenario (Australian study only)
Percentage points difference |
Proportion (95% CI) |
||||||||||
GPs |
Cardiologists |
Other physicians |
|||||||||
Scenario 1 |
|
|
|
||||||||
0–9 |
0.20 (0.15–0.24) |
0.26 (0.13–0.40) |
0.29 (0.23–0.35) |
||||||||
10–19 |
0.27 (0.22–0.32) |
0.29 (0.15–0.42) |
0.34 (0.28–0.40) |
||||||||
20–29 |
0.34 (0.29–0.40) |
0.36 (0.21–0.50) |
0.30 (0.24–0.36) |
||||||||
30+ |
0.20 (0.15–0.24) |
0.10 (0.01–0.18) |
0.07 (0.04–0.10) |
||||||||
Scenario 2 |
|
|
|
||||||||
0–9 |
0.02 (0.01–0.04) |
0.07 (0.00–0.15) |
0.06 (0.03–0.09) |
||||||||
10–19 |
0.02 (0.01–0.04) |
0.05 (0.00–0.11) |
0.03 (0.01–0.05) |
||||||||
20–29 |
0.02 (0.00–0.03) |
0.00 (0.00–0.00) |
0.05 (0.03–0.08) |
||||||||
30+ |
0.94 (0.91–0.97) |
0.88 (0.78–0.98) |
0.86 (0.82–0.91) |
||||||||
Scenario 3 |
|
|
|
||||||||
0–9 |
0.24 (0.19–0.28) |
0.31 (0.17–0.45) |
0.26 (0.21–0.32) |
||||||||
10–19 |
0.29 (0.24–0.34) |
0.45 (0.30–0.60) |
0.33 (0.27–0.39) |
||||||||
20–29 |
0.18 (0.13–0.22) |
0.17 (0.05–0.28) |
0.27 (0.22–0.33) |
||||||||
30+ |
0.30 (0.25–0.35) |
0.07 (0.00–0.15) |
0.13 (0.09–0.17) |
||||||||
Scenario 1: GP v Cardiologist: χ23= 3.01; P = 0.39. GP v Other: χ23= 24.50; P < 0.001. Cardiologist v Other: χ23= 1.13; P = 0.77. Scenario 2: GP v Cardiologist: χ23= 4.80; P = 0.19. GP v Other: χ23= 11.00; P = 0.012. Cardiologist v Other: χ23= 2.78; P = 0.43. Scenario 3: GP v Cardiologist: χ23= 11.09; P = 0.01. GP v Other: χ23= 23.96; P < 0.001. Cardiologist v Other: χ23= 4.33; P = 0.23. |
|||||||||||
5: The spread of estimates given in the Australian and UK studies, shown as quartile boxplots for each scenario. Stars indicate the “correct” estimate
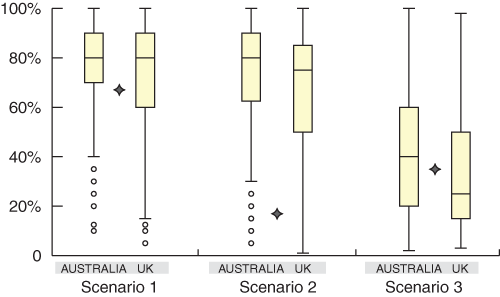
The bottom of each box, the line drawn in the box and the top of the box represent the 1st, 2nd, and 3rd quartiles, respectively (ie, 25%, 50%, and 75% of the data, respectively, lies below these values). The bars (or “whiskers”) at the ends of each box represent the furthest observation lying within 1.5 times the interquartile range (from the first to the third quartile), and any points outside the whiskers are considered outliers.
6: Coefficients (95% CIs) from a linear regression model to identify factors associated with accurate estimation of pre-test probability for all three scenarios (Australian study)*
|
Coefficient (95% CI) |
||||||||||
Scenario 1 |
|
||||||||||
Age |
− 0.09 (− 0.39, 0.20) |
||||||||||
Sex |
− 1.49 (− 3.98, 0.99) |
||||||||||
Country |
1.15 (− 1.68, 3.98) |
||||||||||
School |
0.19 (− 4.90, 5.28) |
||||||||||
Years |
0.23 (− 0.07, 0.52) |
||||||||||
Postgraduate degree (yes v no) |
1.74 (− 0.08, 3.56) |
||||||||||
Practice type (academic v private) |
− 0.28 (− 3.69, 3.13) |
||||||||||
Location (urban v rural) |
− 0.71 (− 3.46, 2.05) |
||||||||||
Practice base (hospital v community) |
− 1.06 (− 3.57, 1.44) |
||||||||||
Profession (cardiologist v GP) |
− 1.39 (− 6.22, 3.44) |
||||||||||
Profession (other physician v GP) |
− 4.01 (− 6.74, − 1.28) |
||||||||||
Constant |
20.09 (7.00, 33.18) |
||||||||||
Scenario 2 |
|
||||||||||
Age |
0.45 (− 0.12, 1.01) |
||||||||||
Sex |
0.65 (− 4.09, 5.39) |
||||||||||
Country |
2.52 (− 2.90, 7.94) |
||||||||||
School |
− 2.01 (− 11.75, 7.72) |
||||||||||
Years |
− 0.15 (− 0.72, 0.41) |
||||||||||
Postgraduate degree (yes) |
4.42 (0.95, 7.89) |
||||||||||
Practice type (academic) |
1.34 (− 5.18, 7.86) |
||||||||||
Location (urban) |
2.99 (− 2.27, 8.24) |
||||||||||
Practice base (hospital) |
1.63 (− 3.14, 6.39) |
||||||||||
Profession (cardiologist) |
0.80 (− 8.43, 10.04) |
||||||||||
Profession (other) |
− 5.44 (− 10.66, − 0.22) |
||||||||||
Constant |
22.55 (− 2.50, 47.59) |
||||||||||
Scenario 3 |
|
||||||||||
Age |
0.21 (− 0.23, 0.66) |
||||||||||
Sex |
3.51 (− 0.29, 7.31) |
||||||||||
Country |
2.25 (− 2.11, 6.60) |
||||||||||
School |
− 2.40 (− 10.17, 5.37) |
||||||||||
Years |
− 0.01 (− 0.46, 0.44) |
||||||||||
Postgraduate degree (yes) |
− 2.00 (− 4.78, 0.78) |
||||||||||
Practice type (academic) |
− 2.84 (− 8.07, 2.40) |
||||||||||
Location (urban) |
2.98 (− 1.22, 7.18) |
||||||||||
Practice base (hospital) |
− 1.65 (− 5.46, 2.17) |
||||||||||
Profession (cardiologist) |
− 2.78 (− 10.15, 4.59) |
||||||||||
Profession (other) |
− 3.15 (− 7.31, 1.01) |
||||||||||
Constant |
14.04 (− 6.03, 34.11) |
||||||||||
* R 2 values for regression models for scenarios 1–3 were 7%, 7%, and 5%, respectively.
Appendix: Example (using Scenario 1) of the feedback given to the respondents
Scenario 1: A 65-year-old man presents to the emergency room of your local hospital having had two episodes of retrosternal chest pain today, both precipitated by exertion, but lasting about 2 hours despite rest. Before obtaining the rest of the history or performing a physical examination, what would you estimate his risk of true ischaemic heart disease to be?
The estimate, derived from the clinical decision rule, was 67%. Questionnaire responses ranged from 10% to 100%, with 24% being within 10 percentage points (on either side) of this estimate. The clinical decision rule is found in the following article:
Diamond GA, Forrester JS. Analysis of probability as an aid in the clinical diagnosis of coronary artery disease. N Engl J Med 1979; 300: 1350-1358.
This study relates the clinical presentation of chest pain to the probability of ischaemic heart disease (IHD) determined by angiography. A critical review of the article reveals some caveats. The authors based their probabilities on a review of the literature, without giving any details about how they searched for articles, what inclusion or exclusion criteria they used, how they extracted and compiled the data, and how they calculated their estimates. Nevertheless, the estimates have stood the test of time, and the study remains one of the best presentations of probabilities of IHD in the literature. The authors classified chest pain according to responses to the following questions:
Is the patient’s chest discomfort retrosternal?
Are the patient’s symptoms brought on predictably by exertion?
Are the symptoms relieved within 30 minutes, or more typically within 2–15 minutes, by rest or nitroglycerine?
“Asymptomatic” is characterised by no positive responses; “non-anginal chest pain” by one positive response; “atypical angina” by two positive responses; and “typical angina” by a positive response to all three questions.
The authors expressed the probabilities of IHD as given in the Table. It is important to note that these estimates relate to hospital presentation and that estimates in primary care may be lower.
Age |
Asymptomatic |
Non-anginal |
Atypical angina |
Typical angina |
|||||||
Men |
Women |
Men |
Women |
Men |
Women |
Men |
Women |
||||
30–39 |
1.9% |
0.3% |
5.2% |
0.8% |
21.8% |
4.2% |
69.7% |
25.8% |
|||
40–49 |
5.5% |
1.0% |
14.1% |
2.8% |
46.1% |
13.3% |
87.3% |
55.2% |
|||
50–59 |
9.7% |
3.2% |
21.5% |
8.4% |
58.9% |
32.4% |
92.0% |
79.4% |
|||
60–69 |
12.3% |
7.5% |
28.1% |
18.6% |
67.1% |
54.4% |
94.3% |
90.6% |
|||
Received 27 March 2003, accepted 9 February 2004
- John R Attia1
- David W Sibbritt2
- Ben D Ewald3
- Balakrishnan R Nair4
- Neil S Paget5
- Rod F Wellard6
- Lesley Patterson7
- Richard F Heller8
- 1 Centre for Clinical Epidemiology and Biostatistics, University of Newcastle, Newcastle, NSW.
- 2 Department of Medicine, John Hunter Hospital, New Lambton, NSW.
- 3 The Royal Australasian College of Physicians, Sydney, NSW.
- 4 Royal Australian College of General Practitioners, South Melbourne, VIC.
- 5 Evidence for Population Health Unit, University of Manchester, Manchester, UK.
None identified.
- 1. None identified.
- 2. Jaeschke R, Guyatt G, Lijmer J. Diagnostic tests. In: Guyatt G, Rennie D, editors. Users’ guides to the medical literature. A manual for evidence-based practice. Chicago: AMA Press, 2002.
- 3. Letelier LM, Weaver B, Montori V. Diagnosis. Examples of likelihood ratios. In: Guyatt G, Rennie D, editors. Users’ guides to the medical literature. A manual for evidence-based practice. Chicago: AMA Press, 2002.
- 4. Richardson WS. Five uneasy pieces about pre-test probability. J Gen Intern Med 2002; 17: 891-892.
- 5. Sackett DL, Haynes RB, Guyatt GH, Tugwell P, editors. Clinical epidemiology. A basic science for clinical medicine. 2nd edition. Boston: Little Brown, 1991: 100.
- 6. Bobbio M, Fubini A, Detrano R, et al. Diagnostic accuracy of predicting coronary artery disease related to patients’ characteristics. J Clin Epidemiol 1994; 47: 389-395.
- 7. Bobbio M, Detrano R, Shandling AH, et al. Clinical assessment of the probability of coronary artery disease: judgmental bias from personal knowledge. Med Decis Making 1992; 12: 197-203.
- 8. Lyman GH, Balducci L. The effect of changing disease risk on clinical reasoning. J Gen Intern Med 1994; 9: 488-495.
- 9. Dolan JG, Bordley DR, Mushlin AI. An evaluation of clinicians subjective prior probability estimates. Med Decis Making 1986; 6: 216-223.
- 10. Diamond GA, Forrester JS. Analysis of probability as an aid in the clinical diagnosis of coronary artery disease. N Engl J Med 1979; 300: 1350-1358.
- 11. Wells PA, Anderson DR, Bormanis J, et al. Value of assessment of pretest probability of deep-vein thrombosis in clinical management. Lancet 1997; 350:1795-1798.
- 12. Wolf PA, D’Agostino RB, Belanger AJ, Kannel WB. Probability of stroke: a risk profile from the Framingham Study. Stroke 1991; 22: 312-318.
- 13. JMP [statistical software], version 4, Cary, NC: SAS Institute Inc, 2001.
- 14. Lipinski M, Do D, Froelicher V, et al. Comparison of exercise test scores and physician estimation in determining disease probability. Arch Intern Med 2001; 161: 2239-2244.
- 15. McManus RJ, Mant J, Meulendijks CFM, et al. Comparison of estimates and calculations of risk of coronary heart disease by doctors and nurses using different calculation tools in general practice: cross sectional study. BMJ 2002; 324: 459-464.
- 16. Noguchi Y, Matsui K, Imura H, et al. Quantitative evaluation of the diagnostic thinking process in medical students. J Gen Intern Med 2002; 17: 848-853.
- 17. Steurer J, Fischer JE, Bachmann LM, et al. Communicating accuracy of tests to general practitioners: a controlled study. BMJ 2002; 324: 824-826.
- 18. Stevens J. Applied multivariate statistics for the social sciences. 3rd edition. Mahwah, NJ: Lawrence Erlbaum Publishers, 1998: 72.
- 19. Shim JH, Haynes RB, Johnson ME. Effect of problem-based, self-directed, undergraduate education on life-long learning. Can Med Assoc J 1993; 148: 969-976.
- 20. Norman GR, Shannon SI. Effectiveness of instruction in critical appraisal skills: a critical appraisal. Can Med Assoc J 1998; 158: 177-181.
- 21. McGettigan P, Sly K, O'Connell D, et al. The effects of information framing on the practices of physicians. J Gen Intern Med 1999; 14: 633-642.
- 22. Brassey J, Elsyn G, Price C, Kinnersley P. Just in time information for clinicians: a questionnaire evaluation of the ATTRACT Project. BMJ 2001; 322: 529-530.
- 23. Stiell IG, McKnight RD, Greenberg GH, et al. Implementation of the Ottawa ankle rules. JAMA 1994; 271: 827-832.
- 24. Stiell IG, Wells GA, Vandemheem KL, et al. The Canadian C-spine rule for radiography in alert and stable trauma patients. JAMA 2001; 286: 1841-1848.





Abstract
Objective: To assess the accuracy and variability of clinicians’ estimates of pre-test probability for three common clinical scenarios.
Design: Postal questionnaire survey conducted between April and October 2001 eliciting pre-test probability estimates from scenarios for risk of ischaemic heart disease (IHD), deep vein thrombosis (DVT), and stroke.
Participants and setting: Physicians and general practitioners randomly drawn from College membership lists for New South Wales and north-west England.
Main outcome measures: Agreement with the “correct” estimate (being within 10, 20, 30, or > 30 percentage points of the “correct” estimate derived from validated clinical-decision rules); variability in estimates (median and interquartile ranges of estimates); and association of demographic, practice, or educational factors with accuracy (using linear regression analysis).
Results: 819 doctors participated: 310 GPs and 288 physicians in Australia, and 106 GPs and 115 physicians in the UK. Accuracy varied from about 55% of respondents being within 20% of the “correct” risk estimate for the IHD and stroke scenarios to 6.7% for the DVT scenario. Although median estimates varied between the UK and Australian participants, both were similar in accuracy and showed a similarly wide spread of estimates. No demographic, practice, or educational variables substantially predicted accuracy.
Conclusions: Experienced clinicians, in response to the same clinical scenarios, gave a wide range of estimates for pre-test probability. The development and dissemination of clinical decision rules is needed to support decision making by practising clinicians.